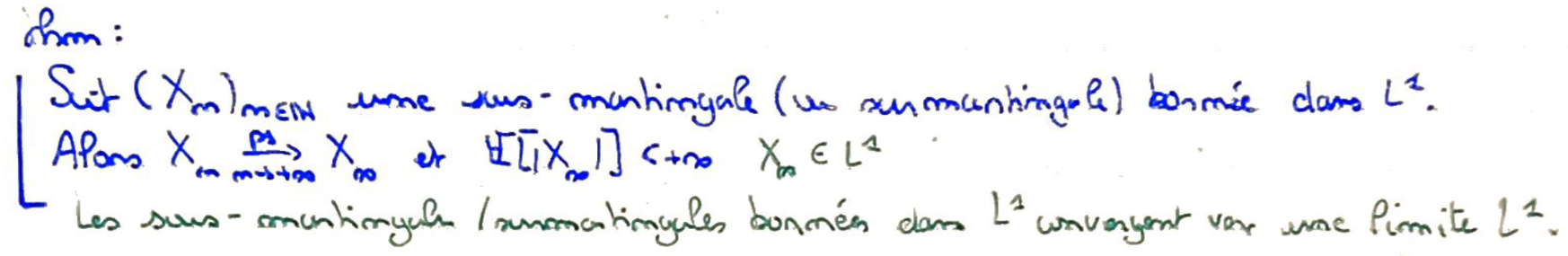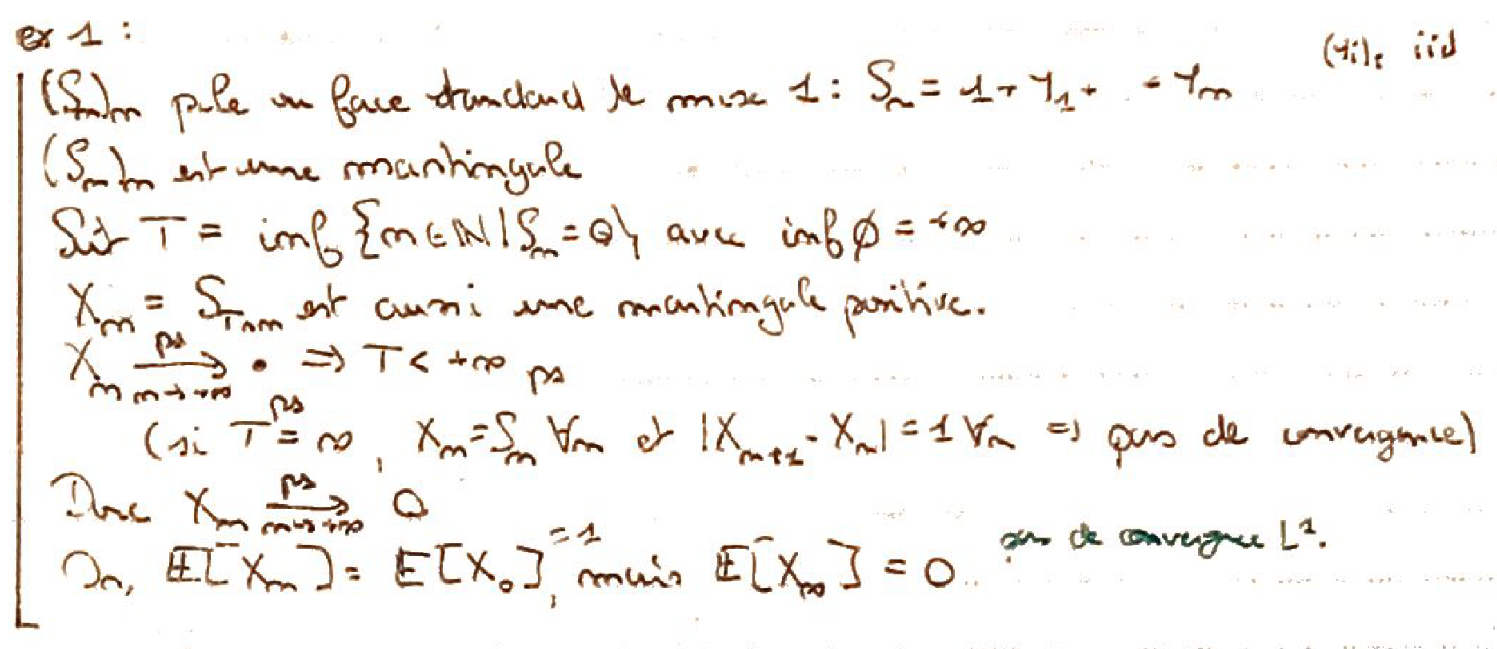Martingale \((X_n)_{n\in\Bbb N}\)
Processus adapté à valeur réelles et \(\in L^1\) pour lequel on a : $$\forall n\in{\Bbb N},\qquad {\Bbb E}[X_{n+1}|{\mathcal F}_n]=X_n.$$
- on dit qu'on a une surmartingale (resp. sous-martingale) si on a à la place de l'égalité l'inégalité \(\leqslant\) (resp. \(\geqslant\))
- interprétation d'une martingale : \(X_n\) représente la fortune d'un joueur à l'instant \(n\) lors d'un jeu équitable
- pour une surmartingale (resp. Sous-martingale), \(X_n\) représente la fortune d'un joueur dans un jeu favorable (resp. Défavorable)
- \((X_n)_{n\in\Bbb N}\) est une surmartingale \(\iff\) \((-X_n)_{n\in\Bbb N}\) est une sous-martingale
- si \((X_n)_{n\in\Bbb N}\) est une martingale, on a \(\forall n\leqslant m\), \({\Bbb E}[X_m|{\mathcal F}_n]=\) \(X_n\) et \(n\mapsto\) \({\Bbb E}[X_n]\) est constante
- si \((X_n)_{n\in\Bbb N}\) est une surmartingale (resp. Sous-martingale), on a \(\forall n\leqslant m\), \({\Bbb E}[X_m|{\mathcal F}_n]\leqslant X_n\) (resp. \(\geqslant\)), et \(n\mapsto {\Bbb E}[X_n]\) est croissante (resp. Décroissante)
- si \((X_n)_{n\in\Bbb N}\) est une martingale et si \(\varphi\) est positive et convexe tq \(\forall n,{\Bbb E}[\varphi(X_n)]\lt +\infty\), alors \((\varphi(X_n))_{n\in\Bbb N}\) est une Sous-martingale
- on a le même résultat si \((X_n)_{n\in\Bbb N}\) est une sous-martingale, à condition que \(\varphi\) soit également croissante
- si \((X_n)_{n\in\Bbb N}\) est une sur/sous-martingale bornée dans \(L^1\), alors \(X_n\overset{ps}{\underset{n\to+\infty}\longrightarrow} X_\infty\in L^1\)
- si \((X_n)_{n\in\Bbb N}\) est une sous-martingale positive, alors on a aussi \(\forall n\in{\Bbb N}, X_n\geqslant {\Bbb E}[X_\infty|{\mathcal F}_n]\) (//Martingale fermée)
- caractérisation des martingales pour lesquelles on a \(X_n\overset{ps,\,L^1}{\underset{n\to+\infty}\longrightarrow} X_\infty\) :
- \((X_n)_n\) est uniformément intégrable
\((X_n)_n\) est une Martingale fermée, avec \(Z=X_\infty\)
- si \((X_n)_n\) est une sous-martingale, et si \(S\leqslant T\) sont deux t.a. bornés, alors \(X_T,X_S\in L^1\), et \({\Bbb E}[X_S]\leqslant{\Bbb E}[X_T]\)
- si \((X_n)_n\) est une martingale bornée dans \(L^p\) avec \(p\gt 1\), alors \(X_n\overset{ps,\,L^p}{\underset{n\to+\infty}\longrightarrow} X_\infty\)
- si on note \(X^*_\infty:=\) \(\sup_{k\geqslant0}\lvert X_k\rvert\), alors \({\Bbb E}[(X_\infty^*)^p]\leqslant(\frac p{1-p})^p{\Bbb E}[\lvert X_\infty\rvert^p]\)
(
Espérance conditionnelle)
Questions de cours
START
Ω Basique (+inversé optionnel)
Recto: Donner un exemple de cas qui vérifie ces hypothèses, mais où on n'a pas la convergence \(L^1\).
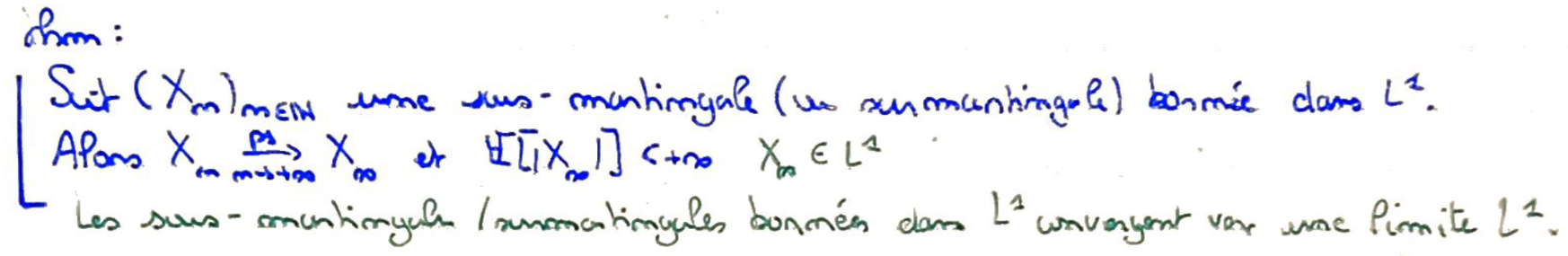

Verso:
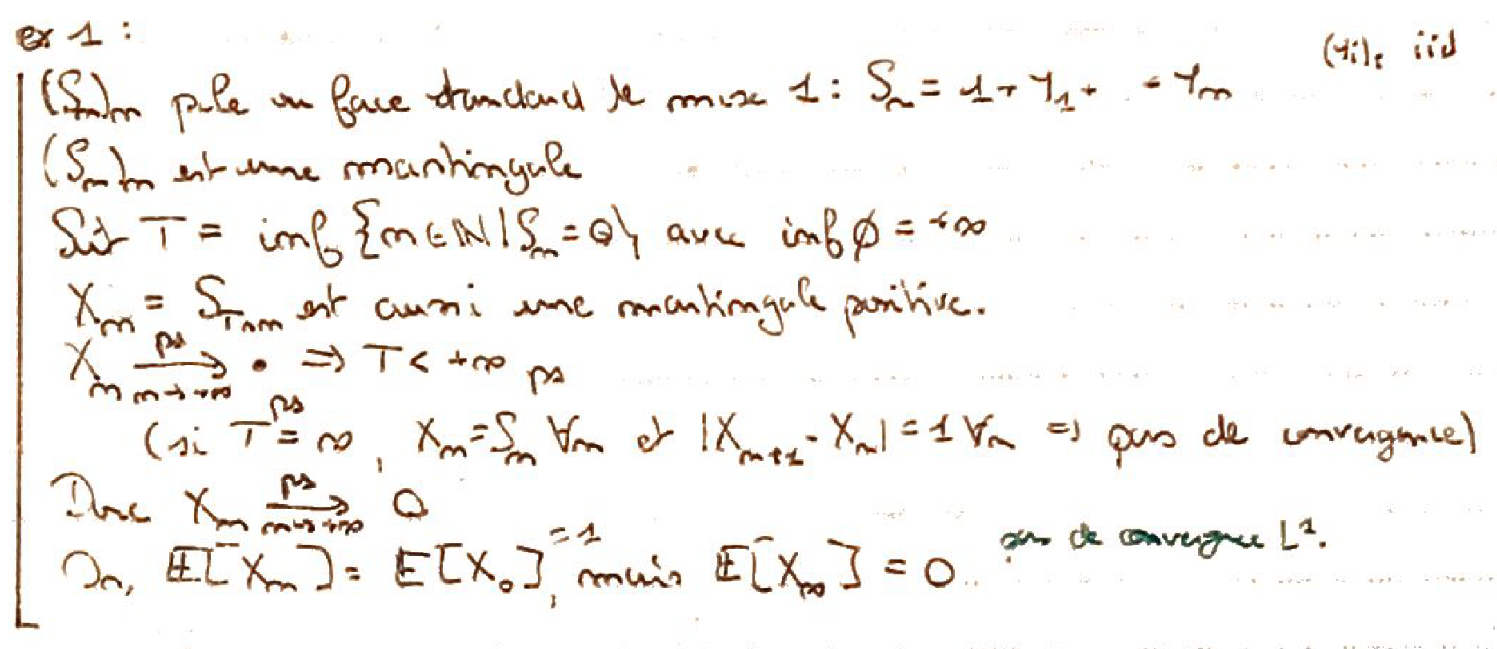
Bonus:
Carte inversée ?:
END
Flashcards
START
Ω Basique (+inversé optionnel)
Recto: A quelle condition a-t-on \(x\mapsto{\Bbb E}[X_n]\) constante ?
Verso: \((X_n)\) doit être une martingale.
Bonus:
Carte inversée ?:
END
START
Ω Basique (+inversé optionnel)
Recto: A quelle condition a-t-on \(\forall n\leqslant m,{\Bbb E}[X_m|{\mathcal F}_n]=X_n\) ?
Verso: \((X_n)\) doit être une martingale.
Bonus:
Carte inversée ?:
END
START
Ω Basique (+inversé optionnel)
Recto: A quelle condition a-t-on \(x\mapsto{\Bbb E}[X_n]\) décroissante ?
Verso: \((X_n)\) doit être une surmartingale.
Bonus:
Carte inversée ?:
END
START
Ω Basique (+inversé optionnel)
Recto: A quelle condition a-t-on \(\forall n\leqslant m,{\Bbb E}[X_m|{\mathcal F}_n]\leqslant X_n\) ?
Verso: \((X_n)\) doit être une surmartingale.
Bonus:
Carte inversée ?:
END
START
Ω Basique (+inversé optionnel)
Recto: A quelle condition a-t-on \(x\mapsto{\Bbb E}[X_n]\) croissante ?
Verso: \((X_n)\) doit être une sous-martingale.
Bonus:
Carte inversée ?:
END
START
Ω Basique (+inversé optionnel)
Recto: A quelle condition a-t-on \(\forall n\leqslant m,{\Bbb E}[X_m|{\mathcal F}_n]\geqslant X_n\) ?
Verso: \((X_n)\) doit être une sous-martingale.
Bonus:
Carte inversée ?:
END
START
Ω Basique (+inversé optionnel)
Recto: Que représente une martingale ?
Verso: Elle représente la fortune d'un joueur à l'instant (tour) \(n\) dans un jeu
équitable.
Bonus:
Carte inversée ?: y
END
START
Ω Basique (+inversé optionnel)
Recto: Que représente une surmartingale ?
Verso: Elle représente la fortune d'un joueur à l'instant (tour) \(n\) dans un jeu
défavorable.
Bonus:
Carte inversée ?: y
END
START
Ω Basique (+inversé optionnel)
Recto: Que représente une martingale ?
Verso: Elle représente la fortune d'un joueur à l'instant (tour) \(n\) dans un jeu
favorable.
Bonus:
Carte inversée ?: y
END
START
Ω Basique (+inversé optionnel)
Recto: A quelle condition \((\varphi(X_n))_n\) est-elle une sous-martingale ?
Verso:
- Soit \((X_n)_n\) martingale, \(\varphi\) positive, convexe et tq \({\Bbb E}[\varphi(X_n)]\lt +\infty\)
- Soit \((X_n)_n\) sous-martingale, \(\varphi\) positive, convexe, tq \({\Bbb E}[\varphi(X_n)]\lt +\infty\) et \(\varphi\) croissante
Bonus:
Carte inversée ?: y
END
START
Ω Basique (+inversé optionnel)
Recto: A quelle condition a-t-on \(X_n\overset{ps}{\underset{n\to+\infty}\longrightarrow} X_\infty\in L^1\) ?
Verso: \((X_n)_n\) doit être une sur/sous-martingale bornée dans \(L^1\).
Bonus:
Carte inversée ?: y
END
START
Ω Basique (+inversé optionnel)
Recto: A quelle condition a-t-on \(\forall n\in{\Bbb N}, X_n\geqslant{\Bbb E}[X_\infty|{\mathcal F}_n]\) ?
Verso: \((X_n)_n\) doit être une sous-martingale positive bornée dans \(L^1\).
Bonus:
Carte inversée ?: y
END
START
Ω Basique (+inversé optionnel)
Recto: A quelle condition a-t-on \(X_n\overset{ps,\,L^1}{\underset{n\to+\infty}\longrightarrow} X_\infty\) ?
Verso: \((X_n)_n\) est une martingale qui doit vérifier l'une des deux conditions équivalentes :
- \((X_n)_n\) est uniformément intégrable
- \((X_n)_n\) est une martingale fermée, avec \(Z=X_\infty\)
Bonus:
Carte inversée ?: y
END
START
Ω Basique (+inversé optionnel)
Recto: A quelle condition a-t-on \({\Bbb E}[X_S]\leqslant{\Bbb E}[X_T]\), avec \(S\leqslant T\) deux temps d'arrêt ?
Verso: \((X_n)_n\) doit être une sous-martingale, et \(S,T\) doivent être bornés.
Bonus:
Carte inversée ?: y
END
START
Ω Basique (+inversé optionnel)
Recto: A quelle condition a-t-on \(X_n\overset{ps,\,L^p}{\underset{n\to+\infty}\longrightarrow} X_\infty\) ?
Verso: On doit avoir \((X_n)_n\) une martingale bornée dans \(L^p\), et \(p\gt 1\).
Bonus:
Carte inversée ?: y
END
START
Ω Basique (+inversé optionnel)
Recto: Comment le
Lemme de Fatou peut-il être utilisé dans un problème avec une martingale et un temps d'arrêt ?
Verso: $${\Bbb E}[X_T\Bbb 1_{T\lt \infty}]={\Bbb E}\left[\underset{n\to+\infty}{\operatorname{lim} } X_{n\land T}\Bbb 1_{T\lt \infty}\right]\leqslant\underset{n\to+\infty}{\operatorname{lim} }{\Bbb E}[X_{n\land T}\Bbb 1_{T\lt \infty}]$$
Bonus:
Carte inversée ?: y
END
Exercices